Altın oran, doğada sayısız canlının ve cansızın şeklinde ve yapısında bulunan özel bir orandır. Doğada bir bütünün parçaları arasında gözlemlenen, yüzyıllarca sanat ve mimaride uygulanmış, uyum açısından en yetkin boyutları verdiği sanılan geometrik ve sayısal bir oran bağıntısıdır. Doğada en belirgin örneklerine insan vücudunda, deniz kabuklularında ve ağaç dallarında rastlanır. Platon'a göre kozmik fiziğin anahtarı bu orandır. Altın oranı bir dikdörtgenin boyunun enine olan "en estetik" oranı olarak tanımlayanlar da vardır.
Eski Mısırlılar ve Yunanlılar tarafından keşfedilmiş, mimaride ve sanatta kullanılmıştır. Göze çok hoş gelen bir orandır.
Altın Oran; CB / AC = AB / CB = 1.618; bu oranın değeri her ölçü için 1.618 dir.
Bir doğru parçasının (AB) Altın Oran'a uygun biçimde iki parçaya bölünmesi gerektiğinde, bu doğru öyle bir noktadan (C) bölünmelidir ki; küçük parçanın (AC) büyük parçaya (CB) oranı, büyük parçanın (CB) bütün doğruya (AB)oranına eşit olsun.
Altın Oran, pi (π) gibi irrasyonel bir sayıdır ve ondalık sistemde yazılışı; 1.618033988749894... dür. (noktadan sonraki ilk 15 basamak). Bu oranın kısaca gösterimi: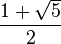 
olur. Altın Oranın ifade edilmesi için kullanılan sembol, PHI yani Φ'dir.
Altın Oran'ı anlatmanın en iyi yollarından biri, işe bir kare ile başlamaktır.
Bir kareyi tam ortasından iki eşit dikdörtgen oluşturacak şekilde ikiye bölelim.
Dikdörtgenlerin ortak kenarının, karenin tabanını kestiği noktaya pergelimizi koyalım. Pergelimizi öyle açalım ki, çizeceğimiz daire, karenin karşı köşesine değsin, yani yarı çapı, bir dikdörtgenin köşegeni olsun.
Sonra, karenin tabanını, çizdiğimiz daireyle kesişene kadar uzatalım.
Yeni çıkan şekli bir dikdörtgene tamamladığımızda, karenin yanında yeni bir dikdörtgen elde etmiş olacağız.
İşte bu yeni dikdörtgenin taban uzunluğunun (B) karenin taban uzunluğuna (A) oranı Altın Oran'dır. Karenin taban uzunluğunun (A) büyük dikdörtgenin taban uzunluğuna (C) oranı da Altın Oran'dır. A / B = 1.6180339 = Altın Oran C / A = 1.6180339 = Altın Oran
Elde ettiğimiz bu dikdörtgen ise, bir Altın Dikdörtgen'dir. Çünkü uzun kenarının, kısa kenarına oranı 1.618 dir, yani Altın Oran'dır.
Artık bu dikdörtgenden her bir kare çıkardığımızda elimizde kalan, bir Altın Dikdörtgen olacaktır.
İçinden defalarca kareler çıkardığımız bu Altın Dikdörtgen'in karelerinin kenar uzunluklarını yarıçap alan bir çember parçasını her karenin içine çizersek, bir Altın Spiral elde ederiz. Altın Spiral, birçok canlı ve cansız varlığın biçimini ve yapı taşını oluşturur.Buna örnek olarak Ayçiçeği bitkisini gösterebiliriz. Ayçiçeğinin çekirdekleri altın oranı takip eden bir spiral oluşturacak şekilde dizilirler.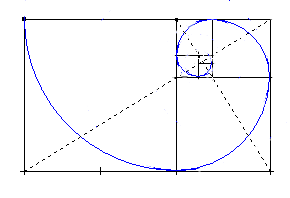 
Bu karelerin kenar uzunlukları sırasıyla Fibonacci sayılarını verir.
